Principe-dimension
20 – « Seigneur, tu as tout réglé avec mesure, nombre et poids. »
Livre de la Sagesse - Chapitre 13
« 01 Ils sont foncièrement insensés, tous ces hommes qui en sont venus à ignorer Dieu : à partir de ce qu'ils voient de bon, ils n'ont pas été capables de connaître Celui qui est ; en examinant ses oeuvres, ils n'ont pas reconnu l'Artisan.
02 Mais c'est le feu, le vent, la brise légère, la ronde des étoiles, la violence des flots, les luminaires du ciel, gouverneurs du monde, qu'ils ont regardés comme des dieux.
03 S'ils les ont pris pour des dieux à cause de la beauté qui les a charmés, ils doivent savoir combien le Maître de ces choses leur est supérieur, car l'Auteur même de la beauté est leur créateur.
04 Et s'ils les ont pris pour des dieux à cause de la puissance et de l'efficacité qui les ont frappés, ils doivent comprendre à partir de ces choses combien Celui qui les a faites est plus puissant.
05 Car la grandeur et la beauté des créatures font, par analogie, découvrir leur Auteur.
06 Et pourtant, ces hommes ne méritent qu'un blâme léger; car ils ne s'égarent peut-être qu'en cherchant Dieu avec le désir de le trouver :
07 ils poursuivent leur recherche en étant plongés au milieu de ses oeuvres, et ils se laissent prendre aux apparences, car ce qui s'offre à leurs yeux est si beau !
08 Encore une fois, pourtant, ils ne sont pas excusables.
09 S'ils ont poussé la science à un degré tel qu'ils sont capables d'avoir une idée sur le cours éternel des choses, comment n'ont-ils pas découvert plus vite Celui qui en est le Maître ?
01 - 05 Versets non traduits dans la version actuelle de la Bible de la liturgie
06 La nuit de la délivrance pascale avait été connue d'avance par nos Pères; assurés des promesses auxquelles ils avaient cru, ils étaient dans la joie.
07 Et ton peuple accueillit à la fois le salut des justes et la ruine de leurs ennemis.
08 En même temps que tu frappais nos adversaires, tu nous appelais pour nous donner ta gloire.
09 Dans le secret de leurs maisons, les fidèles descendants des justes offraient un sacrifice, et ils consacrèrent d'un commun accord cette loi divine :que les saints partageraient aussi bien le meilleur que le pire ; et déjà ils entonnaient les chants de louange des Pères.
10 - 13 Versets non traduits dans la version actuelle de la Bible de la liturgie
14 Un silence paisible enveloppait toute chose, et la nuit de la Pâque était au milieu de son cours rapide ;
15 alors, du haut du ciel, venant de ton trône royal, Seigneur, ta Parole toute-puissante fondit en plein milieu de ce pays de détresse, comme un guerrier impitoyable, portant l'épée tranchante de ton décret inflexible.
16 Elle s'arrêta, et sema partout la mort ; elle touchait au ciel en même temps qu'elle marchait sur la terre. »
Des Nombres
« L’analogie se rapporte à l’usage des proportions et à l’équivalence des rapports qui engendrent des formes semblables récurrentes. La symétrie est prise dans le sens de commensurabilité entre le tout et les parties. » « De Architectura » de Vitruve ( 85 av. J.C – 26 ap. J .C) commensurabilité : grandeurs de même espèces qui peuvent être mesurées par une grandeur commune.
Objet fractal ? Objet sans dimension, expression logarithme qui est un nombre décimal compris entre 0 et 3.
Une fractale est un ensemble géométrique possédant une symétrie particulière. En effet, les parties de cet objet sont les répliques réduites de sa forme globale.
Une fractale est un objet mathématique qui a comme propriété principale d'être identique à lui - même quelle que soit l'échelle d'observation
Les fractales sont définies par une relation de récurrence en chaque point dans un espace.
En mathématiques, la commensurabilité traduit le fait que le rapport entre deux nombres soit nombre rationnel
Il nous est demandé de déterminer les règles de pensées par lesquelles nous pourrons atteindre la vérité, ce qui est véritable, la réalité et non de rendre intelligible tout ce qui existe avec sa raison d’être. La construction est logique et rationnelle.
Dîtes moi comment peut - on subordonner la Raison Universelle ( notion de ceux qui se revendiquent du siècle des lumières) à l’individuelle sans subordonner l’objectivité à la subjectivité et au nom de cette raison dénaturée nier et expulser Celui qu Est de sa création Ils sont moqueurs et contempteurs. Il y a un temps pour tout et leur temps est passé. La raison doit capituler, nous devons avoir confiance. La raison est issue de Dieu. Il a créé et fabriqué le monde.
Que dit la Tradition ? « Les nombres établissent le rapport du Principe à la manifestation. » ou comme le pensait Pythagore : « Tout est ordonné par le Nombre. ». Louis Claude de Saint Martin ne disait – il pas : « Les nombres sont les enveloppes visibles des êtres. »
Ils expriment une « qualité ». Ils sont forces, idées, concepts. Les nombres sont plus vrais que les mots. Ils se rient de notre subjectivité. Ils s’imposent entiers dans le fracas de leur objectivité, dans l’accès à une juste compréhension.
Comme le dit Jésus : « Que celui qui a des oreilles pour entendre, entende ! »
Après tout, chacun est maître de son salut ou de sa perdition. Il vit ou n ’ est « que de la paille à brûler ». En vivant en toute liberté dans la puissance de Celui qui Est , nous éviterons la prévarication, n’en déplaise à tous les adultères qui s’adorent sous l’éclairage illusoire de leurs lumières.
Les chiffres, alors !Les chiffres composent les nombres. Un chiffre seul peut également être un nombre. Ils permettent de compter ou d ‘établir des rapports, entre autre. Ils sont quantités.
Tout est rapport et proportion, me semble être un concept primordial transmis, comme par ailleurs celui de système de référence ou pierre angulaire. Deux ou plusieurs dimensions peuvent donc être liées entre elles par le biais du système de référence s’appuyant sur une structure de base de données déterminée, stockée d’une façon optimale et possédant de bonnes qualités de transmission. En d’autres termes, plus globalement, la géométrie de la forme s’appuie sur la science des Nombres pour se développer.
Un ordre sous-jacent existerait – il ? Le désordre en découlerait-il ? Est-il vraiment désordre ?
Notre monde est donc construit en rapports et proportions avec symétrie. Un rapport est une qualité, non une quantité. Une multitude ou pas de rapports inter agissent entre eux pour créer en proportion dans l’harmonie d’une musique cosmique. Ne serions nous pas également une tendance à exister figée dans une observation ?
Ne peut on pas penser que le message sera déchiffré uniquement dans le cas où l’espèce humaine serait en mesure de le faire ou alors plus justement uniquement par ce qu ‘il en a été décidé.
L'homme calcule depuis 2000 ans avant Jésus-Christ avec 10 chiffres (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), on parle alors de base décimale (ou base 10). Toutefois dans des civilisations plus anciennes ou pour certaines applications actuelles d'autres bases de calcul ont été et sont toujours utilisées :
base sexagésimale (60), utilisée par les Sumériens. Cette base est également utilisée dans le système horaire actuel, pour les minutes et les secondes ;
base vicésimale (20), utilisée par les Mayas ;
base duodécimale (12), utilisée par les anglo-saxons dans leur système monétaire jusqu'en 1960 : un « pound » représentait vingt « shilling » et un « shilling » représentait douze « pences ». Le système d'heure actuel fonctionne également sur douze heures (notamment dans la notation anglo-saxonne) ;
base quinaire (5), utilisée par les Mayas ;
base binaire (2), utilisée par l'ensemble des technologies numériques
Intéressons - nous au zéro.
Il est position et du fait même de celle-ci il indique la valeur pour les nombres placés à sa gauche.
Pour le 0 on peut écrire que rien n’est rien.
Est-il possible d’envisager 00 = 0 , cela le devrait. Mais 00 = 1 à la manière de 20 =1 ?
Le 0 est l’élément primordial car il permet au 8 et à ses multiples de créer. Le 0 leur laisse toute la place à l‘infini. Il est 8 et ses multiples.
Du binaire
Il a été démontré qu'à l'aide d'un interrupteur fermé pour "vrai" et ouvert pour "faux" il était possible d'effectuer des opérations logiques en associant le nombre " 1 " pour "vrai" et "0" pour "faux".
Ce codage est nommé binaire. C'est avec ce codage que fonctionnent les ordinateurs. Il consiste à utiliser deux états (représentés par les chiffres 0 et 1) pour coder les informations
Le système binaire est un système de numération utilisant la base 2. On nomme couramment bit les chiffres de la numération binaire. Ceux ci ne peuvent prendre que deux valeurs, notées par convention 0 et 1.
C'est un concept essentiel de l'informatique. En effet, les processeurs des ordinateurs sont composés de millions de transistors (imprimés sur un circuit électronique) qui chacun ne gère que des bits 0 (« le courant ne passe pas ») et 1 (« le courant passe »).
Un calcul informatique n'est donc qu'une suite d'opérations sur des paquets de 0 et de 1, appelés octets lorsqu'ils sont regroupés par 8.
Le terme bit, c'est-à-dire 0 ou 1 en numérotation binaire est la plus petite unité d'information manipulable par une machine numérique. Il est possible entre autre de représenter physiquement cette information binaire :
par un signal électrique ou magnétique, qui, au-delà d'un certain seuil, correspond à la valeur 1 ;
grâce des composants électroniques qui ont deux états d'équilibre (l'un correspond à l'état 1, l'autre à 0).
Avec un bit il est ainsi possible d'obtenir deux états : soit 1, soit 0.
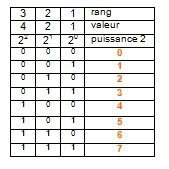
Grâce à 2 bits, il est possible d'obtenir quatre états différents (2*2) :
Valeur 2 bits Valeur décimale
0 0 0
0 1 1
1 0 2
1 1 3
Avec 3 bits, il est possible d'obtenir huit états différents (2*2*2) :
Valeur 3 bits Valeur décimale
0 0 0 0
0 0 1 1
0 1 0 2
0 1 1 3
1 0 0 4
1 0 1 5
1 1 0 6
1 1 1 7
Poids des bits
Dans un nombre binaire, la valeur d'un bit, appelée poids, dépend de la position du bit en partant de la droite. A la manière des dizaines, des centaines et des milliers pour un nombre décimal, le poids d'un bit croît d'une puissance de deux en allant de la droite vers la gauche comme le montre le tableau suivant :
Conversion
Le codage le plus courant est l'équivalent en base deux de la numération de position que nous utilisons quotidiennement en base 10.
Pour convertir un mot binaire en nombre décimal, il suffit de multiplier la valeur de chaque bit(0,1) par son poids, puis d'additionner chaque résultat.
Ainsi, le mot binaire 0101 vaut en décimal :
23x0 + 22x1 + 21x0 + 20x1
= 8 x0 + 4 x1 + 2 x0 + 1 x1 = 5
L'octet
L'octet est une unité d'information composée de 8 bits soit 8 chiffres binaires. Il permet par exemple de stocker un caractère, tel qu'une lettre ou un chiffre.
Ce regroupement de nombres par série de 8 permet une lisibilité plus grande, au même titre que l'on apprécie, en base décimale, de regrouper les nombres par trois pour pouvoir distinguer les milliers. Le nombre « 1 256 245 » est par exemple plus lisible que « 1256245 »
Pour un octet, le plus petit nombre est 0 (représenté par huit zéros 00000000), et le plus grand est 255 (représenté par huit chiffres « un » 11111111), ce qui représente 256 possibilités de valeurs différentes.
11111111= 128 + 64 + 32 + 16 + 8+ 4 + 2 + 1 = 255
00000000= 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 0
L’expression binaire : 11001100 = 128+64+0+0+8+4 = 204
1 on prend la valeur de la colonne ou du « bit »
0 on ne prend pas la valeur ou poids de la colonne ou du « bit »
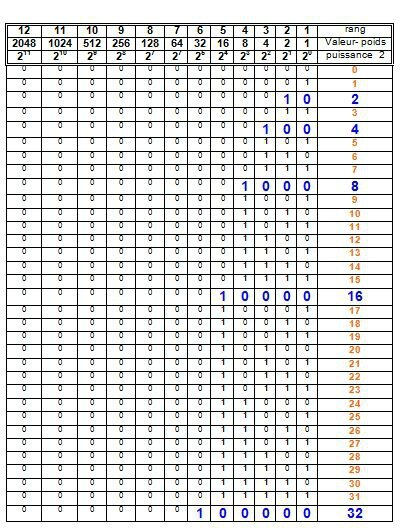
Représentation tableau binaire-décimal base10
Le résultat rouge est la somme des valeurs des colonnes désignées par les 1.
1er colonne 20 = 1 : séquence verticale répétitive 0,1 à l’infini
2ème colonne 21 = 2 : séquence verticale répétitive 0,0,1,1,à l’infini
3ème colonne 22 = 4 : séquence verticale répétitive 0,0,0,0,1,1,1,1, à l’infini
4ème colonne 23 = 8 : séquence verticale répétitive 0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,à l’infini
Cette répartition séquentielle est valable pour toutes les colonnes jusqu’à l’infini. Le nombre de 0 et de 1 par colonne correspond à la valeur même de celle-ci. On commence toujours par le zéro.
Rappels de quelques notions
1 - principe de la base décimale ou base 10
L’idée fondamentale de ce principe réside dans la prédominance de groupement par :
- dizaines ou « paquets » de dix
- centaines ou « paquets » de dix dizaines
- milliers ou « paquets » de dix centaines, etc.
La numérotation écrite actuelle se sert de symboles auxquels on donne le nom de chiffres arabes, à savoir : 1 2 3 4 5 6 7 8 9 0
Ces 9 premiers symboles figurent les unités simples du premier ordre décimal. Ils sont soumis au principe de position puisque leur valeur varie en fonction de la position qu’ils occupent dans l’écriture du nombre. Ainsi 2 peut valoir 2 unités, 2 dizaines ou 2 centaines selon qu’il occupe la 1er, la 2ème ou la 3ème position dans ce genre de représentation chiffrée en partant de la droite vers la gauche.
Quant au zéro il sert à marquer l’absence de chiffre d’un certain ordre ou à exprimer le sens du « nombre nul » qui peut être le résultat d’une opération comme la soustraction d’un nombre par lui - même.
La base dix est le premier nombre représenté au moyen de deux chiffres. Il s’écrit 10 soit 1 dizaine, 0 unité.
Exemples :
11 = 1 dizaine, 1 unité ou dix-un = 10+1
20 = 2 dizaines, 0 unité ou deux-dix = 2*10
100 = 1 centaine, 0 dizaine, 0 unité ou cent = 102
1000 = 1 millier, 0 centaine, 0 dizaine, 0 unité ou mille = 103
10 000 = 1 myriade,0 millier, 0 centaine ,0 dizaine, 0 unité ou myriade = 104
64 632 6 myriades 4 - mille 6 - cent 3 - dix 2
(= 6*10 000 + 4*1000 + 6*100 + 3*10 + 2)
Notons par ailleurs que le zéro correspond à l’un des concepts les plus abstraits que l’homme ait pu imaginer.
2 – principe de la base 2
Le système binaire est un système de numération utilisant la base 2. On nomme couramment bit les chiffres de la numération binaire positionnelle. Ceux-ci ne peuvent prendre que deux valeurs, notées par convention 0 et 1.
Le système binaire le plus courant est l'équivalent en base deux de la numération de position que nous utilisons quotidiennement en base dix.
Dans ce type de codage, chaque nombre est représenté (de façon unique) par une combinaison de puissances de la base. Si on se limite dans un premier temps aux nombres entiers positifs,
en base dix ces puissances sont : 10n
un (1), dix (représenté par 10), cent (dix fois dix, représenté par 100), mille (dix fois cent, représenté par 1000), dix mille (10 fois mille, représenté par 10 000) etc. ;
en base deux, ces puissances sont : 2n
un (1), deux (représenté lui aussi par 10), quatre (deux fois deux, représenté par 100), huit (deux fois quatre, représenté par 1000), seize (deux fois huit, représenté par 10000) etc.
On voit que la signification des représentations 10, 100, 1000, etc. dépend de la base utilisée : 10 est toujours égale à la base, c'est-à-dire dix en base dix, mais deux en base deux []
En base dix, on a besoin de dix chiffres, de zéro à neuf ; et en base deux, on a besoin de seulement deux chiffres : zéro et un.
Chaque 1 représente la valeur verticale de la colonne.
Le résultat rouge est la somme horizontale des valeurs de 1.
Les nombres s'organisent dans la Bible autour de la formule 10n /5n = 2n soit 10n = 5n*2n
Il s'agit de la conversion d'une base 10 en base 2
qui correspond à la dimension binaire-décimale base 10 des 1 et 0, celle de la Bible, à celle numérique base 2 (développement des puissances de 2). Globalement il s’agit d’une écriture décimale positionnelle.
Pour retourner dans les puissances de 2 (développement des puissances de 2) en application de la formule, nous devons simplifier ou diviser chaque tranche de 10 ou multiple de 5 par 5, ce qui donne :
pour 5000 biblique : 5/5*10/5*10/5*10/5 = 5000/625 = 8 = 5/51* 103//53 Nous retrouvons la formule.
5 000 = 5*1000 = 5*10*10*10
pour 25 000 biblique : 25*10*10*10 = 5*5*10*10*10
convertissons : 5/5*5/5*10/5*10/5*10/5 = 25 000/3 125 = 8 = 25/52 * 103/53 Nous retrouvons la formule.
Ex : 5000 = 5*1000 = 5*53*8 = 54*8.
Le résultat est 5000/ 54 = 8. Résultat tout ce qu’il y a de plus normal car le nombre binaire- décimal 10 000 est égal à 16 numérique base 2 c’est à dire le double de 5000 et de 8.
25 000 = 25 * 1000 = 25*5*5*5*8 = 5*5*5*5*5*8= 55 * 8
La valeur numérique base 2 de 25 000 = 25 000 / 55 = 8.
Nous calculons que 25 000 et 5000 = 8. Echelle différente ?
Nous appliquons toujours la même formule à savoir : 10n / 5n = 2n
Effectuons quelques opérations :
2*5 = 10
4*5 = 20 - 20*5 = 100
8*5 = 40 - 40*5 = 200 – 200*5 = 1000
16*5 = 80 - 80*5 = 400 – 400*5 = 2000 – 2000*5 = 10000
En multipliant les puissances de 2 par 5 et ses puissances nous retrouvons l’expression binaire d’origine, à savoir : 2n * 5n = 10n
écrite autrement : 10n/5n = 2n
20*50 = 1*1 = 1
21*51= 2*5 = 10
22*52 = 4*25 = 100
23*53 = 8*125 = 1000
24*54 = 16*625 = 10 000
Raymond Terrasse dans « Mathématiques secrètes de la croix templière » a parfaitement compris. « C’est uniquement de cette façon que l’on aborde les Nombres portés par la Tradition en ne tenant pas compte des unités car ils se situent en amont de ce monde observé et mesuré. Apprendre à compter autrement apporte une compréhension du message transmis entre autre par l ‘ Ancien Testament. Il est nécessaire de dégager les nombres de cette première couverture symbolique nécessaire qui montre leur importance, qui les ancre dans la mémoire collective transmissible pour leur donner une existence en tant qu’objets mathématiques. Ainsi ils nous ouvrent la porte à une compréhension symbolique encore plus puissante qui nous montre, qui nous rapproche, qui nous donne des signes. En dehors de toutes unités, nous nous retrouvons dans le système numérique porté par la Tradition, l’Ancien et le Nouveau Testament. »
Les nombres sont des multiples de 8
Intéressons - nous à la séquence verticale répétitive à l’infini de couleur rouge.
Elle correspond à la somme des 3 premières colonnes ou des 3 « bits »
La somme des 3 « bits » ou 3 colonnes donne une autre unité ou pierre d’achoppement qui est une séquence : 0,1,2,3,4,5,6,7
Nous retrouvons notre chandelier à 7 branches qui a en fait 8 lumières en comptant le zéro. Peut-être la 8ème lumière de Hanoukka ?
Tous les nombres sont des multiples de 8 ou 23.
Pour composer la suite des nombres entiers en utilisant la pierre angulaire ou racine des nombres ou système de référence ( séquence 0,1,2,3,4,5,6,7 ) nous ajoutons à chacun de ses composants un multiple de 8 selon la formule n*23 ( n appartient aux nombres entiers naturels)
Comme ils sont tous multiples de 8 :
Pour n = 0 ( 8*0 =0) : 0+0=0 0/8 = 0
0+1=1 1/8 = 0,125
0+2=2 2/8 = 0,25
0+3=3 3/8 = 0,375
0+4=4 4/8 = 0,50
0+5=5 5/8 = 0,625
0+6=6 6/8 = 0,75
0+7=7 7/8 = 0,875
Pour n=1 (8*1=8) : 8+0 = 8 8/8 = 1
8+1 = 9 9/8 = 1,125
8+2 =10 10/8 = 1,25
8+3 =11 11/8 = 1,375
8+4 =12 12/8 = 1,5
8+5 =13 13/8 = 1,625
8+6 =14 14/8 = 1,75
8+7 =15 15/8 = 1,875
Ainsi jusqu’à l’infini (0,8,16,24,32,40,48,56,64…..) soit [ n* 23 ;(+); (0,1,2,3,4,5,6,7) ]
Le système de numération octal est le système de numération de base 8, et utilise les chiffres de 0 à 7.
Nouvelle représentation
Pour n = 0 ( 8*0 =0) : 0+0=0 0/8 = 0 = 0*0,125 = 0
0+1=1 1/8 = 0,125 = 1*0,125 = 0,125
0+2=2 2/8 = 0,25 = 2*0,125 = 0,25
0+3=3 3/8 = 0,375 = 3*0,125 = 0,375
0+4=4 4/8 = 0,50 = 4*0,125 = 0,5
0+5=5 5/8 = 0,625 = 5*0,125 = 0,625
0+6=6 6/8 = 0,75 = 6*0,125 = 0,75
0+7=7 7/8 = 0,875 = 7*0,125 = 0,875
diviser par 8 = multiplier par 0,125 ( 8/8 = 8*0,125)
Pour n=1 (8*1=8) : 8+0 = 8 8/8 = 1
8+1 = 9 9/8 = 1,125
8+2 =10 10/8 = 1,25
8+3 =11 11/8 = 1,375
8+4 =12 12/8 = 1,5
8+5 =13 13/8 = 1,625
8+6 =14 14/8 = 1,75
8+7 =15 15/8 = 1,875
nombre / 23 = nbre multiple de 8 ; valeur position
ex : 12. 12/8 = 1,5 soit 1 fois 8 + 0,5 valeur position 0,5 = 4 soit 8+4 = 12
10,5 10,5/8 = 1,3125 = 1 fois 8 + valeur position 0,3125/0,125 = 2,5 = 8+2,5 = 10,5
Le dénombrement des séquences verticales multiples de 8 correspond aux valeurs prises successivement par n de n*23 sans tenir compte de la position 0.
Ex : 127 / 8 = 15,875 ; 15 est la 15ème séquence verticale ou autre ou tout système ( en fonction de son stockage) multiple de 8 qui correspond à 15*8 = 120 qui s’additionne à 7 valeur indiquée par 0,875 ( 7/8 = 0,875 de la base 0,1,2,3,4,5,6,7).
Les Nombres développent une métaphore qui donne une représentation mentale d’un processus qui dépasse l’entendement. Aussi doivent – ils être abordés d’une façon littérale.
La dimension binaire détermine horizontalement la valeur éclatée d’un nombre alors que la dimension des Entiers la détermine verticalement simplifiée.
10 = 2 10 = 21
100 = 4 10*10 = 22
1000 = 8 10*10*10 = 23
10 000 = 16 10*10*10*10 = 24
100 000 = 32 10*10*10*10*10 = 25
1 000 000 = 64 10*10*10*10*10*10 = 26
10 000 000 = 128 10*10*10*10*10*10*10 = 27
100 000 000 = 256 10*10*10*10*10*10*10*10 = 28
Les nombres entiers correspondent donc à l’addition binaire non faite de 1et seulement à leur somme.
1
10 = 2
100 = 20 = 4
1000 = 200 = 40 = 8
10 000 = 2000 = 400 = 80 =16
100 000 = 20000 = 4000 = 800 =160 = 32
1 000 000 = 200000 = 40000 = 8000 =1600 = 320 =64
10 000 000 = 2000000 = 400000 = 80000 =16000 =3200 =640 =128
100 000 000= 20000000= 4000000= 800000=160000 =32000 =6400=1280=256
Construisons ce système sur 1 octet expressions binaire-décimale en rouge (jusqu’à 128 soit 27 sans prendre en compte 100 et 20 = 1) et plus jusqu’à 29 en divisant par 2 puis par 10.
/2 /10 /2 /10
1 000 000 000 512 1 000 000 000 100 000 32 100 000
500 000 000 256 100 000 000 50 000 16 10 000
250 000 000 128 10 000 000 25 000 8 1000
125 000 000 64 1 000 000 12 500 4 100
62 500 000 32 100 000 6 250 2 10
31 250 000 16 10 000 3 125 1 1
15 625 000 8 1 000
7 812 500 4 100
3 906 250 2 10
1 953 125 1 1
100 000 000 256 100 000 000 10 000 16 10 000
50 000 000 128 10 000 000 5 000 8 1000
25 000 000 64 1 000 000 2 500 4 100
12 500 000 32 100 000 1 250 2 10
6 250 000 16 10 000 625 1 1
3 125 000 8 1000
1 562 500 4 100
781 250 2 10
390 625 1 1
10 000 000 128 10 000 000 1000 8 1000
5 000 000 64 1 000 000 500 4 100
2 500 000 32 100 000 250 2 10
1 250 000 16 10 000 125 1 1
625 000 8 1000
312 500 4 100
156 250 2 10
78 125 1 1
1 000 000 64 1 000 000 100 4 100
500 000 32 100 000 50 2 10
250 000 16 10 000 25 1 1
125 000 8 1000
62 500 4 100
31 250 2 10 10 2 10
15 625 1 1 5 1 1
10n /2n avec n de 2n {0 …n, n = à n de 10n } = 5n
ou 10n / 5n = 2n, opérations réalisées par paliers ou tranche de 10.
1 jour vaut 1000 ans
1 vaut 1000 vaut 8
1 vaut 10*10*10
convertissons : 1 vaut 10/5*10/5*10/5
1 vaut 2*2*2 = 8
1jour vaut 8
calcul pratique : 1 000 000, expression binaire vaut 64, mais 1 000 000 = 1000*1000 = 8*8 = 64
1 000 000 000, expression binaire de 512 mais 1 000 000 000 = 1000*1000*1000 = 8*8*8 = 512
100 000, expression binaire de 32 mais 100 000 = 100*1000 = 100*8 = 800 = 8*100 = 8*4 = 32
etc, etc. …. avec toutes les combinaisons possibles de multiples de 10.
1 jour vaut 1000 ans
1 vaut 1 an
1 an = 360 car année biblique a une valeur numérique de 360
convertissons : 360 = 36*10 = 36*10/5 = 36*2 = 72
1jour vaut 72
1 jour vaut 1000ans
1 vaut 1000*ans
1 an biblique = 360 jours
1000*360 = 360 000 = 36*10*10*10*10
convertissons : 36*10/5*10/5*10/5*10/5 = 36*16 = 576 ou 1000/53 * 360/5 = 8*72
1jour vaut 576
Apocalypse
1260 jours pour les Témoins de Dieu.
Les nations fouleront la ville sainte pendant : 42mois (42mois / 12 mois = 3,5 ans)
1260/30 = 42 mois
1260/360 = 3,5 ans
1 année biblique a la valeur numérique 360.
1 mois biblique a la valeur numérique 30
Calculs réalisés à partir des mesures bibliques
Tableau de mesures
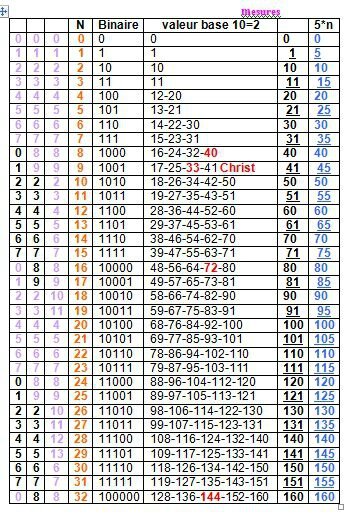
Ex. : 144 est égal à 100 + 40 + 4 = 10*10 + 4*10 + 4 = 10*2 + 4*2 + 4 = 20 + 8 + 4 = 32
Comment pouvons nous compter et en même temps exprimer l’entier naturel en rouge et son équivalent binaire composé de 1 et de 0 ?
Nous devons utiliser les nombres de la colonne de couleur verte, à savoir : 0,1,10,11,20,21,30,31,40,41,50,51, et ceci à l'infini.
Rappelons que 10 binaire = 2 base 2. Pourquoi ? Par ce que la dimension binaire a une structure décimale.
Ex. : 40 = 4*10 = 4*2 =8 40 = 8 et 1000
0=0, 1=1, 10 = 2 et 10, 11 = 3 et 11, 20 = 4 et 100, 21=5 et 101, 30 = 6 et 110,
31 = 7 et 111, 40 = 8 et 1000, 41 = 9 et 1001 –
Utilisons la mesure 144
Cette mesure peut être considérée comme une mesure décimale codée binaire
Afin de concilier la logique binaire avec la logique humaine, on peut convertir en binaire, plutôt que les nombres eux-mêmes, chacune des composantes du nombre qui les construisent en notation décimale positionnelle.
144 se situe dans une dimension intermédiaire entre les valeurs décimales des entiers naturels et les valeurs binaires-décimales des 0 et 1.
10 = 2 et 10/5 = 2 sont les paramètres de référence de cette dimension.
Ex : 10 = 10*1 = 1*2 = 2
100 = 10*10 = 10*2 = 20
1000 = 100*10 = 100*2 = 200
60 = 6*10 = 6*2 = 12
144 est égal à :
100 + 40 + 4 =
10*10 + 4*10 + 4*1 =
10 * 2 + 4 * 2 + 4*1 =
20 + 8 + 4 = 32 ou 140 + 4 = 14*10/5 + 4 = 14*2 + 4 = 28 + 4 = 32
vérification : 144/2 = 72 donc 32/2 = 16
effectivement : 72 = 7*10 + 2*1 = 7*2* + 2*1 = 14 + 2 = 16
Nous ne convertissons qu’une seule fois les différentes composantes du nombre 144 car il se termine par un chiffre différent du 0 et du 5. Autrement nous aurions effectué toutes les conversions permises.
Ex : 150 15*10/5 = 15*2 = 30 3*10/5 = 3*2 = 6
ou 15*10 15/5 * 10/5 = 3*2 = 6
Il est impératif de respecter les degrés de conversion et d’arrêter le processus lorsque l’un des composants du nombre atteint la valeur décimale.
Ex: 120 = 100 + 20 = (10*2 ) + (2*2) = 20+4 = 24
4 est le degré de conversion, tout stoppe, on réalise la conversion du nombre en 24.
En poursuivant la conversion nous ne respecterions pas l’intention du calcul et l’objectif final du résultat escompté.
24 = 20 + 4 = 2*10 + 4 = 2*2 + 4 = 8 la base 10 binaire- décimale = 2 décimal.
Le degré de conversion croit avec le développement des puissances de 2.
Le degré dernier de conversion est la 1ère valeur de la puissance de 2 obtenue par une des composantes du nombre.
Il est impératif de connaitre la dimension de calcul.
Exemple significatif
Jérusalem Céleste
Apocalypse de Jean – chapitre 21 – La nouvelle Jérusalem
«………. Elle avait une haute et grande muraille. Elle avait 12 portes, et sur les portes 12 anges, et des noms écrits, ceux des 12 tribus des fils d’Israël : à l’orient 3 portes, au nord 3 portes, au midi 3 portes, et à l’occident 3 portes. La muraille de la ville avait 12 fondements, et sur eux le 12 noms des 12 apôtres de l’agneau ……Celui qui me parlait avait pour mesure un roseau d’or, afin de mesurer la ville, ses portes, et la muraille. La ville avait la forme d’un carré, et sa longueur était égale à sa largeur. Il mesura la ville avec le roseau et trouva 12 000 stades ; la longueur , la largeur et la hauteur en étaient égales. Il mesura la muraille, et trouva 144 coudées, mesure d’homme, qui était celle de l’ange. »
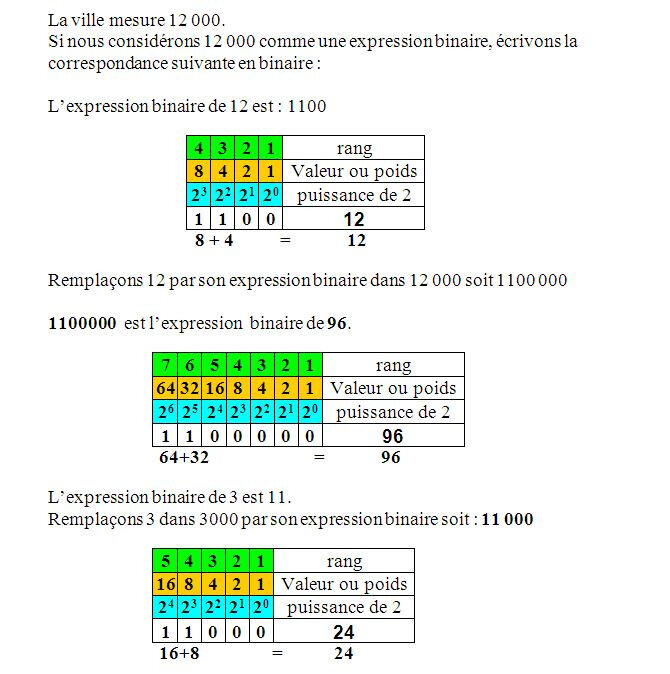
La ville mesure 12 000 stades. Occultons l’unité.
Si nous considérons 12 000 comme une expression binaire, écrivons la correspondance suivante en binaire : 1100 000 ou 1100 (binaire) = 12, entier naturel
1100000 expression binaire correspond à 96 décimal ou 12*8 = 96 puisque 1000 = 8.
En mesure biblique : 12 000 = 12*10*10*10
Convertissons : 12*10/5*10/5*10/5 = 12*2*2*2 = 96
3 000 = 3*1000 = 3*8 = 11 000= 24 puisque 3 = 11 expression binaire.
Le côté d’un carré représentant la ville vaut : 96/4 = 24 et chaque porte vaut : 24/3 = 8
La longueur, la largeur et la hauteur sont égales. Nous avons un cube de 24 de côté.
La valeur numérique de Jérusalem céleste est de 24*24*24 = 13 824
Chaque côté de Jérusalem céleste vaut 12 000/4 = 3 000= 3*10*10*10= 3*5*2*5*2*5*2
Convertissons 3*10/5*10/5*10/5 = 3*2*2*2 = 3*8 = 24
En mesure biblique : 12 000 = 12*10*10*10 = 12*5*2*5*2*5*2
Convertissons : 12*10/5*10/5*10/5 = 12*2*2*2 = 96
Gloire à Son Nom

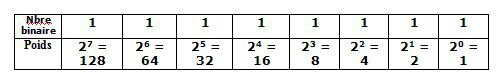







/http%3A%2F%2Fstorage.canalblog.com%2F33%2F62%2F1193778%2F111675983_o.jpg)
/image%2F1371202%2F20240315%2Fob_7c1724_capture476.JPG)
/http%3A%2F%2Fstorage.canalblog.com%2F01%2F70%2F1193778%2F131645305_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F62%2F72%2F1193778%2F131403725_o.jpg)